Accelerometer Guide: Difference between revisions

From Phidgets Support
No edit summary
 
(9 intermediate revisions by 3 users not shown)
Line 1: Line 1:
<metadesc>Accelerometers can be used to measure tilt, vibration and acceleration. Check out our accelerometers and learn more at Phidgets.com.</metadesc>
{{#seo:|description=Discover the basics of accelerometers with this guide. Learn what accelerometers measure, what the measurements mean, how to choose an accelerometer, and more.}}
[[Category:Primer]]
{{#seo:|keywords=accelerometer}}
<!--[[Image:MOT1100.jpg|link=|400px]]-->
[[Category:IntroGuide]]
__TOC__
{{TOC limit|3}}
==Accelerometers and Their Uses==
===Introduction===
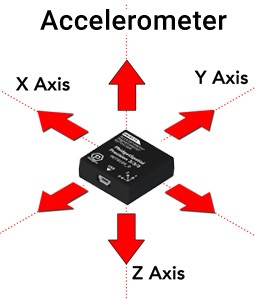
[[File:Accelerometer_Intro.jpg|400px|link=|thumb|Accelerometers Measure Acceleration in 3 Axes]]
As the name implies, accelerometers are devices that measure acceleration. Knowing moment-to-moment accelerations in your system can be useful in tracking motion, orientation, and even vibrations in your system.


==Introduction==
===What the Readings mean===
[[File:1043_1B.jpg|right|link=|400px]]
Accelerometers measure acceleration. As such, you might expect an accelerometer to measure the acceleration of the sensor relative to the space around it, and that if the sensor is standing still it should read 0g. This is not entirely accurate. On the earth’s surface an accelerometer that’s not moving will register a reading of 1G (9.81m/s), straight upwards. So what’s going on here?
An accelerometer is a device that is used to measure acceleration in a given axis.  Often, several accelerometers are combined to create multi axis accelerometers. The accelerometers that we sell are 3-axis accelerometers capable of measuring acceleration in all 3 spatial axes. Typically accelerometers report their measurements in terms of g-force or g's which represents the acceleration in increments of Earth's standard gravitational acceleration (9.81 m/s<sup>2</sup>). A stationary object experiences 1g of acceleration due to the Earth's gravitational field. For reference, a high-speed roller coaster typically develops 4g to 5g, while instantaneous (short duration) g-forces in a car crash can be as high as 100g.
Accelerometers work by measuring the movements of small internal structures caused by accelerating the sensor in a particular direction. When an accelerometer is stationary on earth’s surface, the sensing part of the accelerometer (as with everything else) wants to fall at 1G towards the centre of the earth. However, it is being held up by the casing of the accelerometer by an equivalent 1G in the other direction. Thus, the equivalent measured acceleration is 1G away from the ground.
The only time an accelerometer will register 0G in all directions is if it is in freefall in a vacuum.


Accelerometers can be used for:
===Tilt Angle===
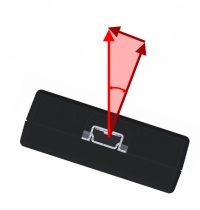
*Detecting the presence of motion and taking basic quantitative measurements. For example, detecting if a bus is moving, and how aggressively the driver is driving.
[[File:Accelerometer_TiltAngle.jpg|200px|link=|thumb|Accelerometers can be used to measure tilt angles]]
*Inertial navigation: estimating speed and position from acceleration.
This constant measuring of acceleration due to gravity makes accelerometers an excellent way to keep track of which way is up. If you want to track a tilt angle, accelerometers can be a very useful tool.
*Measuring a repetitive motion or vibration over a long period of time. For example, finding the vibration modes of a large building.
Where available, you can use the [[Spatial_Primer|Spatial]] object to get pitch and roll angles directly from the Phidgets libraries.
*Measuring tilt. Note: In a static system, you only require an accelerometer - preferably one with high resolution and low noise. In a dynamic system which is moving around, this requires tracking rotation with gyroscopes and/or compasses.


===Tracking Movement===
While it can be tempting to think it would be fairly straightforward to use an accelerometer to keep track of the position of an object over time, the problem of tracking absolute position with an accelerometer turns out to be hard enough that it falls outside of what we can recommend attempting without serious research.


==Gravity vs. Acceleration==
===Vibrations===
It's very important to understand the acceleration that accelerometers measure.
Accelerometers can be used to measure the frequency and amplitude of vibrations. A decent accelerometer can be used to measure acceleration effects small enough to be imperceptible to humans, such as detecting seismic events, or measuring the resonant frequency of a building.


Visualize you are floating weightless in a spaceship in deep space. An accelerometer will show no acceleration (0 g). You strap into your seat, and the rockets fire, accelerating the spaceship (and you) at 9.8 m/s<sup>2</sup> (1 g). The accelerometer will show 1g of acceleration. The acceleration creates the physical impression of weight/gravity. Accelerometers cannot distinguish between the feeling of weight that you feel when you are accelerated (your speed changes), and the steady pull of gravity.
The range of frequencies and amplitudes of vibrations you can measure depend of the speed and noise level of the accelerometer. For best results, you will want to ensure your accelerometer has a data rate at least 4x faster than the frequency of the fastest vibrations you are interested in. You will also want to ensure the noise floor of your sensor is significantly smaller than the signal you expect.  


Stated in a different way - accelerometers do not measure acceleration due to changes in velocity. Rather, they experience '''Proper Acceleration''' - the phenomenon of weight experienced by a test mass that resides in the accelerometer device. On Earth, if the accelerometer is sitting on a surface, completely immobile, it will register a non-zero acceleration (gravity).  If the device is in free fall it will measure no acceleration.
====High Frequency Vibrations====
If you install your accelerometer on, for example, a piece of machinery that is strongly vibrating at frequencies faster than your accelerometer can measure, this can result in aliasing effects and offsets that will throw off your measurements. If you expect the structure you are measuring is likely to produce high frequency vibrations, we recommend isolating your accelerometer from these vibrations using some sort of shock mount. These are typically simple parts made of rubber, elastics or springs, designed to dampen the vibrations that can make it to your sensor.


An accelerometer at rest relative to the Earth's surface will indicate approximately 1g upwards (Because in order to remain at rest, it is experiencing a force opposite to the Earth's gravity- this is called the ''normal force''). To obtain the acceleration due to motion with respect to the Earth, this 'gravity offset' must be subtracted. The effects of this acceleration are indistinguishable from any other acceleration experienced by the instrument, so an accelerometer cannot detect the difference between sitting in a rocket on the launch pad, and being in the same rocket in deep space while it uses its engines to accelerate at 1g. For similar reasons, an accelerometer will read zero during any type of free fall in a vacuum.  When free falling through air, the air resistance produces drag forces that reduce the acceleration, until constant terminal velocity is reached. At terminal velocity the accelerometer will indicate 1g acceleration upwards. For the same reason a skydiver, upon reaching terminal velocity, does not feel as though he or she were in 'free-fall', but rather experiences a feeling similar to being supported (at 1g) on a 'bed' of uprushing air.
===Qualitative Measurements===
[[File:Accelerometer_DeskTapping.jpg|400px|link=|thumb|You can easily spot the time I'm tapping on my desk]]
On the other end of the spectrum, accelerometers can be used for much more basic purposes, such as detecting the fact that an object is moving, or that it’s met a sudden stop. Installed in a car, one might use an accelerometer to consider if one driver drives more aggressively than another. These types of applications that are only interested in getting a general characterization of movement will likely not need high-end sensors to make broad generalizations of the types of movement.


In order to correct for gravity you will need to [[Accelerometer Primer#Calculating tilt angle (roll and pitch) from acceleration|determine the tilt angle]] and subtract 1g in that axis. This means that if you want to measure dynamic acceleration, you can only be sure that you'll be able to measure 1g less than your accelerometer's rated range, since gravity can contribute up to 1g to the measurement and cause the accelerometer to reach its saturation value at a lower acceleration. When the accelerometer saturates, an error will be generated in your program telling you that the value is out of range. For some applications this isn't a big deal, for instance in a remotely controlled vehicle whose accelerometer saturates at a value that can only be reached when the vehicle crashes.
===Choosing an Accelerometer===
The accelerometer or spatial device you use in your application will depend on how accurate certain aspects of your measurement need to be. To simplify the decision, we can narrow this down to various kinds of applications:


==Noise==
{|
Accelerometer chips will always be effected by some amount of noise, usually caused by thermal and mechanical fluctuations inside the sensor. Noise levels will be different for each axis, because each orientation of sensor is built slightly differently (for example, it is much more difficult to get low noise from the vertical axis because the sensor is a flat piece of silicon. Two of the major types of noise are white noise and random walk.
! Application !! Recommended Phidget
 
|-
===White Noise===
| Vibration Measurement || [{{SERVER}}/?prodid=1269 MOT0100 PhidgetAccelerometer]
White noise is the short-term noise that is contributed to from a number of internal and external factors. For example, when an accelerometer is stationary on your desk, it might read 1.00g one sample, 0.99g another sample, and 1.02g in yet another sample. Luckily, white noise is usually fairly consistent which means it can be mitigated quite effectively if you average multiple samples together. With our accelerometers, if you select a data rate slower than its maximum it will automatically average as many samples as it can within that time frame for each value. In applications where you need an extremely fast sampling rate, and can't afford to spend time averaging samples, you should look for an accelerometer with low white noise. Also keep in mind the noisiness of your environment- For example, the engine and road noise on a bus will easily be more noisy than the accelerometer - so there is no point in paying for a low noise accelerometer. See the [[Allan Deviation Primer]] for more information on accelerometer noise characteristics.
|-
 
| Navigation || [{{SERVER}}/?prodid=1205 MOT0110 PhidgetSpatial Precision 3/3/3]
 
|-
===Random Walk===
| Gestures and Qualitative Effects || [{{SERVER}}/products.php?product_id=MOT1102 MOT1102 Spatial Phidget]
Often called drift, random walk is the long-term noise that causes samples to gradually become further and further away from their true values. This type of noise is less important for applications with constant movement and a fast sampling rate, but for applications where values are averaged over longer periods of time, it can cause severe inaccuracies. See the [[Allan Deviation Primer]] for more information on accelerometer noise characteristics.
|}
 
===Accuracy===
[[File:rotationplatform.jpg|thumb|link=|500px|The rotation platform we use to calibrate our accelerometers and spatial devices. The device being calibrated is secured within the aluminium plates at the top, and the platform rotates on all three axes.]]
 
Accuracy is how close the measured value is to the actual physical property being measured. A sensor with very high resolution and low noise may be returning a very precise (but wrong) answer. When we measure the accuracy of our accelerometers, we average a large number of samples together, which allows us to reduce the effects of short-term noise and get a good idea of how accurate they really are. Accuracy is determined by measuring gravity on the accelerometer (1g) as it is held still in different orientations at room temperature.
 
Each accelerometer we sell is individually calibrated. Although this does not remove all errors, the remaining error is non-linear and device specific. If you need higher accuracy, you will only find it in higher end devices, such as aerospace specific accelerometers.


==Demonstrations Using the Control Panel Example==
To more clearly see the effects we have been describing, we can use the Control Panel example for your Phidgets Accelerometer to do some demonstrations.


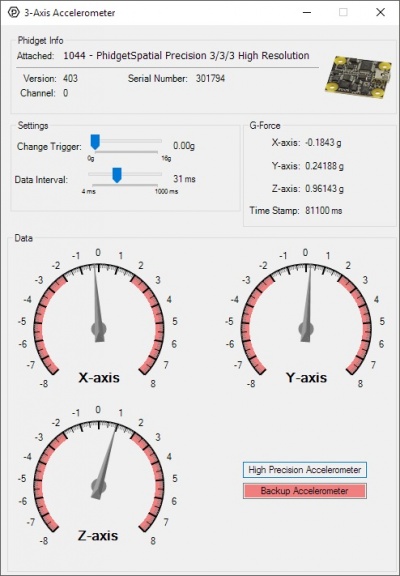
==Calculating tilt angle (roll and pitch) from acceleration==
[[File:Accelerometer_Example.jpg|400px|link=|thumb|The Phidgets Control Panel Accelerometer Example]]
One thing people commonly want to determine with an accelerometer is the physical orientation of the object the device is mounted on.  This can be done by calculating the tilt angle of the accelerometer board. This is possible due to gravity providing a constant acceleration which can be checked against, meaning we can break the total acceleration down into components and then perform a bit of math to obtain a tilt angle. Tilt angle can only be measured when the accelerometer is stationary. When in motion, the acceleration experienced by the accelerometer is a combination of the device’s physical orientation, and the device’s movement, and the tilt can therefore not be determined.  The tilt is calculated as follows-


:<math>Tilt = (arcsin(g_x))^\circ a_x + (arcsin(g_y))^\circ a_y</math>
Once your example is open, we recommend sliding the DataInterval slider all the way to the left for the highest data rates from your sensor.


Where
If your sensor supports temperature stabilization, a checkbox will be available to enable heating. For best results, check the box to enable heating and wait for the temperature measurement to turn green.
:<math>g_x</math> = acceleration in the x-axis
:<math>g_y</math> = acceleration in the y-axis
:a = indicates which axis the tilt is in


With the example open, and the DataInterval set as fast as the sensor will go, try moving the sensor around and observe the dials on the example. Each dial corresponds to the acceleration in one axis of movement.


Example of tilt angle calculation:
To better visualise this, place the sensor right-side up and flat. You should see the Z axis give a reading of +1. Flip the device over, and Z will read -1. If you instead point the cable at the ground, Y will read -1, with X and Z reading 0. Flip the device so that the cable is pointing skywards, and Y will read 1. Likewise with X: pointing the cable at yourself, right-side upwards will give +1, left -1.
{|class="wikitable" style="text-align:center; width: 50%;margin:auto"
|style="background:#f0f0f0;"|'''Axis'''
|style="background:#f0f0f0;"|'''Measured Acceleration (g's)'''
|-
|x || 0.25
|-
|y|| -0.73
|-
|}


By rotating the sensor slowly between these axes, you can see how the reading shifts between these axes. In this way, trigonometry can be used to calculate the angle of the device relative to the ground using the strengths of all the axes, so long as the device is not in motion. This behaviour is used in the [[Spatial_Primer|Spatial]] object to calculate pitch and roll of the sensor.


:<math>Tilt = (arcsin(g_x))^\circ a_x + (arcsin(g_y))^\circ a_y</math>
Similarly, as you move the sensor around, the axes will measure the overall acceleration in their corresponding directions, which can be used to gain a general sense of the sensor’s movement. Of course, if the sensor is rotating at all, the acceleration data alone can’t tell us much more than the fact that the sensor is moving, but that’s a topic for another time.
::<math>Tilt = 14.48^\circ a_x - 46.89^\circ a_y</math>


When you are looking to use the accelerometer to measure translational acceleration, you will need to calibrate the accelerometer to account for the tilt angle or you will get skewed results.
===Vibrations===
To get a sense of just how sensitive your accelerometer can be to vibrations, you can open the graphing tool for the Z-axis.
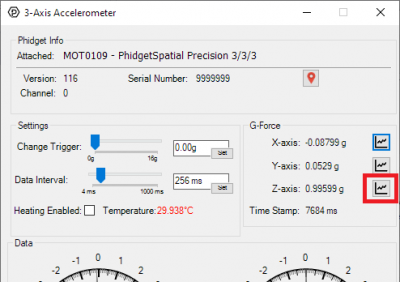
[[File:Open_Accelerometer_Graph.jpg|400px|link=|center|thumb|Click the graph icon to open the graph for the given axis]]


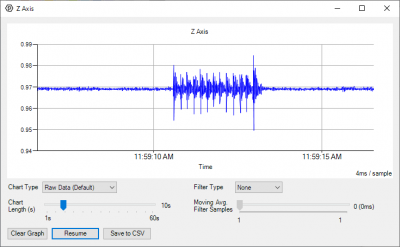
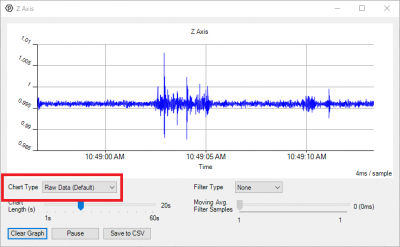
==Calculating Velocity and Position from Acceleration==
From the time graph that shows by default, you can see the readings from the axis over time. By placing the sensor on my desk, I can see the vibrations caused by my typing on the keyboard as wider sections of the graph. You can try this for yourself by placing the sensor on a flat surface, and tapping the surface somewhere else.
You can use integrals to estimate velocity from a set of acceleration values. Likewise, if you integrate a set of velocity values, you'll end up with an estimate of the position. Many programming languages have built-in libraries for integration. You'll need to keep track of the data values and the timestamps of each whenever an acceleration change occurs.  
[[File:Open_Accelerometer_FFT_Graph.jpg|400px|center|thumb|Choose FFT to see frequency data]]


==High Frequency Vibrations==
Now comes the really cool part: if you change your graph to FFT mode, you can see a readout of all the frequencies measured by the sensor. We won’t cover the specifics of how Fourier transforms work here, but it’s applying math to the readings that turns time-based signals into a collection of frequencies that make up the signal.
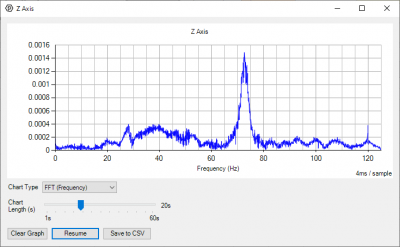
Harsh vibration will cause the sensor to resonate at very high frequencies - not the frequencies you are trying to measure.  This resonance appears on the output as on offset, and is impossible to filter out. The vibration can often be felt - if your application has a metal chassis with motors attached, there is a good chance the chassis will vibrate strongly when the motors are moving. The accelerometer will have to be isolated from the vibration, using vibration mounts. Vibration mounts are simple parts made of rubber, springs, or other elastic materials that can help dampen vibrations to whatever is mounted on them.  


==Choosing an Accelerometer==
[[File:Accelerometer_FFT_Graph.jpg|400px|link=|thumb|FFT Frequency Data of Tapping a Desk]]
The first question to ask when selecting an appropriate accelerometer is ''How precise do you need the measurements to be?'' Do you just need to sense 'when' an object is moving, with no particular emphasis on the strength of the movement, or do you need accurate data for calculations? You can cut a lost of costs if you only need a basic accelerometer.  
'''Note:''' ''Fourier transforms are not natively available from the Phidgets libraries outside of the graphing function. If you want to use frequency data in your program, we recommend finding a Fourier transform library for your programming language.''


Another important criteria is the type of acceleration you're trying to measure. Are they brief, high-acceleration 'shocks' of movement, or gradual, moderate acceleration? The answer to this question will determine the type of noise characteristics you're looking for in an accelerometer. The former lends itself to accelerometers with low white noise, since white noise can't be averaged out over many samples if only a few samples reflect the event being measured. The latter is better suited to an accelerometer with low random-walk (also known as drift), since the white noise can be easily averaged out. See the [[Allan Deviation Primer]] for more information on noise characteristics.
By tapping my desk in Fourier transform mode, my graph shows a peak between 70-75Hz, which would be the resonant frequency of my desk.


If you're using the accelerometer to measure high-frequency vibrations, you want to pay attention to the bandwidth of your device. Accelerometers will measure up to a particular frequency of acceleration (easiest to understand as a vibration). Bandwidth specifies the maximum frequency at which the accelerometer will only 'see' 50% of the acceleration. To achieve a particular bandwidth in your application - say you want to measure a vibration or motion with acceleration up to 100Hz, your accelerometer should be rated for at least 150Hz bandwidth (>50% higher), and have a sampling rate of at least 400 samples per second (4x higher).
The same can be done on the X and Y axes, to see the components of vibration for all axes.
Interestingly, if you solidly mount your accelerometer to a vibrating surface, you can calculate how far that surface is moving in each direction by integrating the motion over time, though the specific calculations are outside the scope of this document.


If you're using the accelerometer as part of a navigation system, you may benefit from adding a gyroscope and compass to aid in calculations. You can keep things simple by getting all three components on one board. Have a look at the [{{SERVER}}/?tier=1&catid=10&pcid=8 Motion] category on our website to see a list of accelerometers, spatials and other motion-related sensors.
The number at the far right of the graph is the highest frequency the device is mathematically capable of measuring. Any frequency components higher than this will result in aliasing. In a broad sense, the math is unable to distinguish between higher frequency signals and those on the graph, making higher frequency signals look like some other frequency that does fit on the graph. The specifics of how this works are outside the scope of this document, but the main takeaway is that if you are interested in measuring the frequency of vibrations, the vibrations in your system that make it to your sensor should be limited to those less than the maximum frequency measurable by your sensor.

Latest revision as of 17:22, 16 January 2024

Accelerometers and Their Uses

Introduction

Accelerometers Measure Acceleration in 3 Axes

As the name implies, accelerometers are devices that measure acceleration. Knowing moment-to-moment accelerations in your system can be useful in tracking motion, orientation, and even vibrations in your system.

What the Readings mean

Accelerometers measure acceleration. As such, you might expect an accelerometer to measure the acceleration of the sensor relative to the space around it, and that if the sensor is standing still it should read 0g. This is not entirely accurate. On the earth’s surface an accelerometer that’s not moving will register a reading of 1G (9.81m/s), straight upwards. So what’s going on here? Accelerometers work by measuring the movements of small internal structures caused by accelerating the sensor in a particular direction. When an accelerometer is stationary on earth’s surface, the sensing part of the accelerometer (as with everything else) wants to fall at 1G towards the centre of the earth. However, it is being held up by the casing of the accelerometer by an equivalent 1G in the other direction. Thus, the equivalent measured acceleration is 1G away from the ground. The only time an accelerometer will register 0G in all directions is if it is in freefall in a vacuum.

Tilt Angle

Accelerometers can be used to measure tilt angles

This constant measuring of acceleration due to gravity makes accelerometers an excellent way to keep track of which way is up. If you want to track a tilt angle, accelerometers can be a very useful tool. Where available, you can use the Spatial object to get pitch and roll angles directly from the Phidgets libraries.

Tracking Movement

While it can be tempting to think it would be fairly straightforward to use an accelerometer to keep track of the position of an object over time, the problem of tracking absolute position with an accelerometer turns out to be hard enough that it falls outside of what we can recommend attempting without serious research.

Vibrations

Accelerometers can be used to measure the frequency and amplitude of vibrations. A decent accelerometer can be used to measure acceleration effects small enough to be imperceptible to humans, such as detecting seismic events, or measuring the resonant frequency of a building.

The range of frequencies and amplitudes of vibrations you can measure depend of the speed and noise level of the accelerometer. For best results, you will want to ensure your accelerometer has a data rate at least 4x faster than the frequency of the fastest vibrations you are interested in. You will also want to ensure the noise floor of your sensor is significantly smaller than the signal you expect.

High Frequency Vibrations

If you install your accelerometer on, for example, a piece of machinery that is strongly vibrating at frequencies faster than your accelerometer can measure, this can result in aliasing effects and offsets that will throw off your measurements. If you expect the structure you are measuring is likely to produce high frequency vibrations, we recommend isolating your accelerometer from these vibrations using some sort of shock mount. These are typically simple parts made of rubber, elastics or springs, designed to dampen the vibrations that can make it to your sensor.

Qualitative Measurements

You can easily spot the time I'm tapping on my desk

On the other end of the spectrum, accelerometers can be used for much more basic purposes, such as detecting the fact that an object is moving, or that it’s met a sudden stop. Installed in a car, one might use an accelerometer to consider if one driver drives more aggressively than another. These types of applications that are only interested in getting a general characterization of movement will likely not need high-end sensors to make broad generalizations of the types of movement.

Choosing an Accelerometer

The accelerometer or spatial device you use in your application will depend on how accurate certain aspects of your measurement need to be. To simplify the decision, we can narrow this down to various kinds of applications:

Application Recommended Phidget
Vibration Measurement MOT0100 PhidgetAccelerometer
Navigation MOT0110 PhidgetSpatial Precision 3/3/3
Gestures and Qualitative Effects MOT1102 Spatial Phidget

Demonstrations Using the Control Panel Example

To more clearly see the effects we have been describing, we can use the Control Panel example for your Phidgets Accelerometer to do some demonstrations.

The Phidgets Control Panel Accelerometer Example

Once your example is open, we recommend sliding the DataInterval slider all the way to the left for the highest data rates from your sensor.

If your sensor supports temperature stabilization, a checkbox will be available to enable heating. For best results, check the box to enable heating and wait for the temperature measurement to turn green.

With the example open, and the DataInterval set as fast as the sensor will go, try moving the sensor around and observe the dials on the example. Each dial corresponds to the acceleration in one axis of movement.

To better visualise this, place the sensor right-side up and flat. You should see the Z axis give a reading of +1. Flip the device over, and Z will read -1. If you instead point the cable at the ground, Y will read -1, with X and Z reading 0. Flip the device so that the cable is pointing skywards, and Y will read 1. Likewise with X: pointing the cable at yourself, right-side upwards will give +1, left -1.

By rotating the sensor slowly between these axes, you can see how the reading shifts between these axes. In this way, trigonometry can be used to calculate the angle of the device relative to the ground using the strengths of all the axes, so long as the device is not in motion. This behaviour is used in the Spatial object to calculate pitch and roll of the sensor.

Similarly, as you move the sensor around, the axes will measure the overall acceleration in their corresponding directions, which can be used to gain a general sense of the sensor’s movement. Of course, if the sensor is rotating at all, the acceleration data alone can’t tell us much more than the fact that the sensor is moving, but that’s a topic for another time.

Vibrations

To get a sense of just how sensitive your accelerometer can be to vibrations, you can open the graphing tool for the Z-axis.

Click the graph icon to open the graph for the given axis

From the time graph that shows by default, you can see the readings from the axis over time. By placing the sensor on my desk, I can see the vibrations caused by my typing on the keyboard as wider sections of the graph. You can try this for yourself by placing the sensor on a flat surface, and tapping the surface somewhere else.

Choose FFT to see frequency data

Now comes the really cool part: if you change your graph to FFT mode, you can see a readout of all the frequencies measured by the sensor. We won’t cover the specifics of how Fourier transforms work here, but it’s applying math to the readings that turns time-based signals into a collection of frequencies that make up the signal.

FFT Frequency Data of Tapping a Desk

Note: Fourier transforms are not natively available from the Phidgets libraries outside of the graphing function. If you want to use frequency data in your program, we recommend finding a Fourier transform library for your programming language.

By tapping my desk in Fourier transform mode, my graph shows a peak between 70-75Hz, which would be the resonant frequency of my desk.

The same can be done on the X and Y axes, to see the components of vibration for all axes. Interestingly, if you solidly mount your accelerometer to a vibrating surface, you can calculate how far that surface is moving in each direction by integrating the motion over time, though the specific calculations are outside the scope of this document.

The number at the far right of the graph is the highest frequency the device is mathematically capable of measuring. Any frequency components higher than this will result in aliasing. In a broad sense, the math is unable to distinguish between higher frequency signals and those on the graph, making higher frequency signals look like some other frequency that does fit on the graph. The specifics of how this works are outside the scope of this document, but the main takeaway is that if you are interested in measuring the frequency of vibrations, the vibrations in your system that make it to your sensor should be limited to those less than the maximum frequency measurable by your sensor.

Retrieved from "https://www.phidgets.com/docs/index.php?title=Accelerometer_Guide&oldid=34330"